RLC直列回路の過渡現象

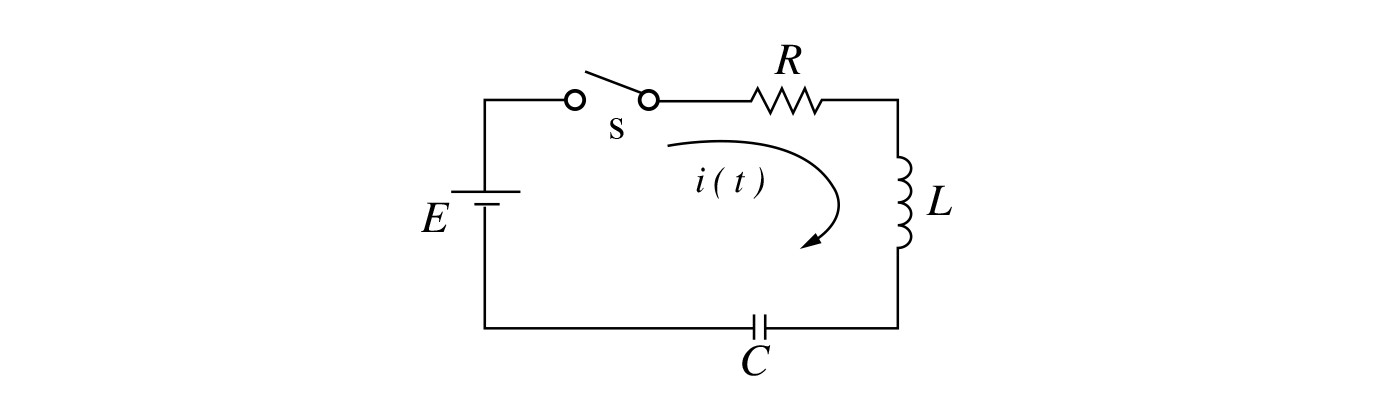
インダクタンスLとキャパシタンスCの両者が含まれている回路においては、磁気エネルギーと静電エネルギーの間に、相互変換がおこなわれ、印加した電圧が直流であっても、応答電流は振動的になることがある。 RLC直列回路に、t=0でスイッチを閉じて、直流電圧Eを印加する。回路に成立する微･積分方程式は、

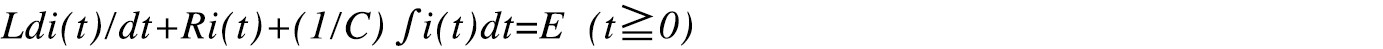
となる。ここで、電流を電荷で置き換えると、i(t)=rq(t)/dtである、よって、

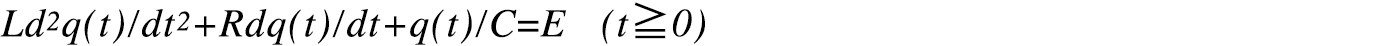
この式は、2階の線形非同次方程式である。同次方程式に解q(t)=q0ε^-λtを代入して、

この結果、q(t)≢0として、

ここで、R⋛4L/Cに応じて、非振動（過制動）、臨界制動、振動の場合に分けられる。ただし、

とする。