RL直列回路の過渡現象

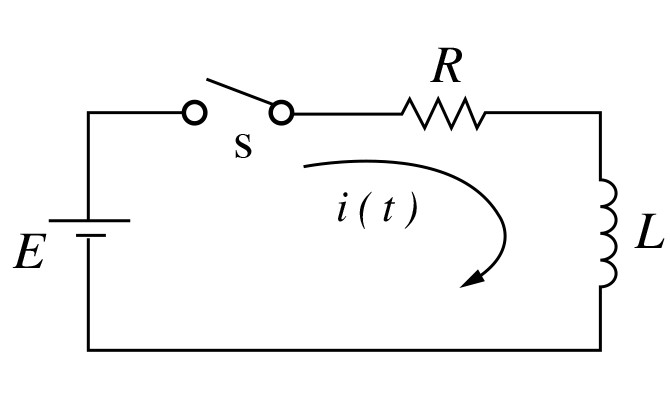
RL直列回路において、t=0にスイッチSを閉じて、直流電圧Eを印加する。回路方程式は、

である。この微分方程式を解けば、回路を流れる電流が求められる。同次方程式(E=0とした場合)の解は、

に、解i_t(t)=i₀ε^-λtを仮定して代入すると、

が得られる。ε^-λt≠0であるから、-λL+R=0が成立しなければならない。よって、

となる。非同次方程式の解は、

であるから、初期条件i(0)=0を用いて、

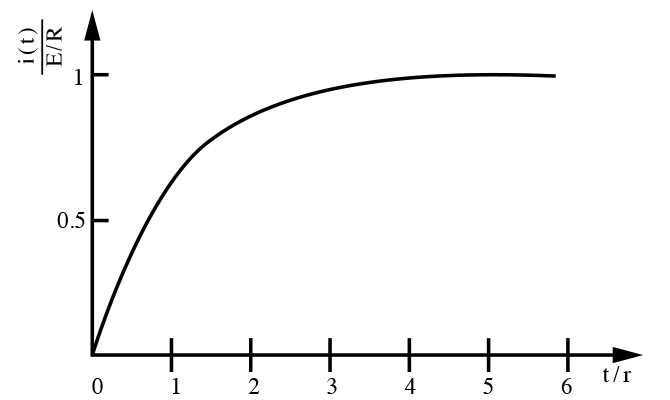
となる。ここで、τ=L/Rを時定数という。